지구에서 거리재기
turf.js의 distance에서는 Haversine formula를 사용하고 있고 이를 이해하기 위해 이것저것 찾아보던 중 지구에서 두 점 사이의 거리 구하기라는 글과 이 글의 원문인 Calculate distance, bearing and more between Latitude/Longitude points을 보았습니다. 이 글에서 Haversine formula를 사용하는 방법 외에도 다양한 두 점 사이의 거리를 구하는 방법을 소개하고 있어서 한번 살펴보고자 합니다.
Haversine formula
먼저 살펴볼 방법은 Haversine formula를 사용하는 방법입니다. Haversine 공식은 전에 작성한 Distance에서도 한번 정리하였지만, 간단하게 다시 정리하자면 두 점(P, Q) 사이의 각 는 두 점의 , 경도(latitude)와 , 위도(longitude)에 대해 다음과 같은 공식이 성립합니다.
앞선 공식에서 대치할 수 있는 부분들을 대치하면 다음과 같이 정리할 수 있습니다.
도출한 공식을 코드로 작성한다면 다음과 같습니다.
function distanceByHaversineFormula(from, to) {
const R = 6371e3;
const lon1 = from[0];
const lat1 = from[1];
const lon2 = to[0];
const lat2 = to[1];
const φ1 = (lat1 * Math.PI) / 180;
const φ2 = (lat2 * Math.PI) / 180;
const Δφ = ((lat2 - lat1) * Math.PI) / 180;
const Δλ = ((lon2 - lon1) * Math.PI) / 180;
const h = Math.pow(Math.sin(Δφ / 2), 2) + Math.pow(Math.sin(Δλ / 2), 2) * Math.cos(φ1) * Math.cos(φ2);
return R * 2 * Math.atan2(Math.sqrt(h), Math.sqrt(1 - h));
}Spherical Law of Cosines
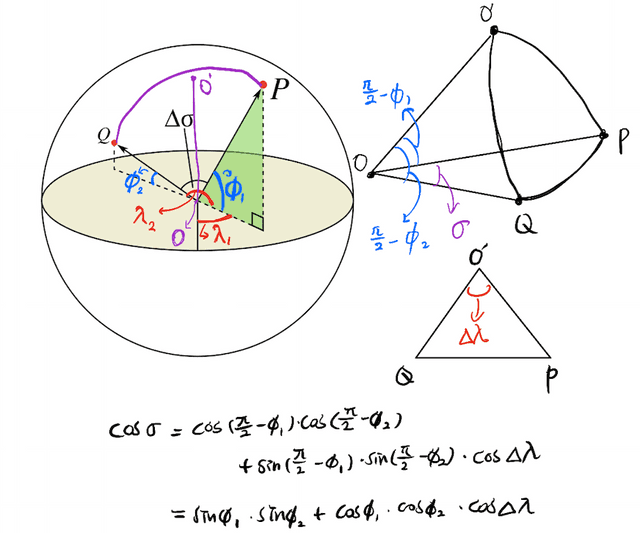
두 번째로 살펴볼 방법은 Spherical Law of Cosines를 사용하는 방법입니다. 구면 코사인 법칙에 의하여 두 점(P, Q) 사이의 각 는 두 점의 , 경도(latitude)와 , 위도(longitude)에 대해 다음과 같은 공식이 성립합니다.
이 공식과 실제 구현에서 사용하고 있는 수식이 차이가 있어 어떻게 도출되었는지 확인해보고자 직접 그려보며 확인해보았습니다. 다음과 같이 두 점 P, Q와 북극점을 바탕으로 도출된 것으로 보입니다.
도출한 공식을 코드로 작성한다면 다음과 같습니다.
function distanceBySphericalLawOfCosines(from, to) {
const R = 6371e3;
const lon1 = from[0];
const lat1 = from[1];
const lon2 = to[0];
const lat2 = to[1];
const φ1 = (lat1 * Math.PI) / 180;
const φ2 = (lat2 * Math.PI) / 180;
const Δλ = ((lon2 - lon1) * Math.PI) / 180;
return R * Math.acos(Math.sin(φ1) * Math.sin(φ2) + Math.cos(φ1) * Math.cos(φ2) * Math.cos(Δλ));
}Equirectangular approximation
세 번째로 살펴볼 방법은 Equirectangular approximation를 사용하는 방법입니다. 정방형 근사를 사용하는 방식은 두 점을 정방형 투영하여 피타고라스의 정리를 사용하는 방법입니다. 다소 오차가 발생하겠지만 짧은 거리만 사용한다면 정확도는 떨어지지만, 더 높은 성능을 확보할 수 있습니다. (자오선을 따라 오류가 없다고 합니다.)
두 점의 , 경도(latitude)와 , 위도(longitude)에 대해 다음과 같이 도출됩니다. (은 경도의 평균입니다.)
도출한 방식을 코드로 작성한다면 다음과 같습니다.
function distanceByEquirectangularApproximation(from, to) {
const R = 6371e3;
const lon1 = from[0];
const lat1 = from[1];
const lon2 = to[0];
const lat2 = to[1];
const Δλ = ((lon2 - lon1) * Math.PI) / 180;
const Δφ = ((lat2 - lat1) * Math.PI) / 180;
const φm = (((lat2 + lat1) * Math.PI) / 180) * 0.5;
const x = Δλ * Math.cos(φm);
const y = Δφ;
return R * Math.sqrt(x * x + y * y);
}비교
서울, 뉴욕을 기준으로 호출했을 때 세 방식에 대한 결과는 다음과 같습니다. Haversine 공식과 구면 코사인 법칙은 유사한 값을 반환했지만, 구면 코사인 법칙이 더 빨리 결과를 내주었습니다. 속도 측면에서는 정방형 근사가 제일 빨랐지만, 다른 두 값에 비해 상당히 다른 값을 반환하였습니다.
HaversineFormula : 11052555.8503412, 95.041 micro seconds
SphericalLawOfCosines : 11052555.850341197, 31.917 micro seconds
EquirectangularApproximation : 17337148.1737011, 25.666 micro seconds서울, 수원을 기준으로 호출했을 때 세 방식에 대한 결과는 다음과 같습니다. 세 방식 모두 유사한 값을 내어주었고, 전반적으로 속도도 먼 거리보다 빠르게 나왔습니다.
HaversineFormula : 32343.763840874522, 4.666 micro seconds
SphericalLawOfCosines : 32343.763840997413, 2 micro seconds
EquirectangularApproximation : 32343.76451538824, 1.458 micro seconds세 방식 중 정사형 근사가 정확도는 떨어지지만 가장 빨랐고, 구면 코사인 법칙이 정확도 유사하지만, Haversine 공식에 비해 속도가 빨랐습니다. 원문에서는 구면 코사인 법칙이 조금 더 느린 것으로 언급되었지만, 연산의 복잡도가 더 적기 때문에 구면 코사인 법칙이 더 빠르게 나온 것으로 생각됩니다.
다만, 구면 코사인 법칙 대신 Haversine 공식을 쓰는 이유는 부동소수점 문제를 해결하기 위해 Haversine 공식에서 arcsine 대신 arctangent를 사용했던 것 처럼 arccos를 사용하는 구면 코사인 법칙도 부동소수점 문제가 발생하기 때문이 아닐까 생각합니다.
다음과 같이 Haversine 공식에서 arcsine 대신 arctangent를 사용하게 하였을 경우에는 구면 코사인 법칙과 유사한 속도를 보여줍니다.
function distanceByHaversineFormulaAndAsin(from, to) {
const R = 6371e3;
const lon1 = from[0];
const lat1 = from[1];
const lon2 = to[0];
const lat2 = to[1];
const φ1 = (lat1 * Math.PI) / 180;
const φ2 = (lat2 * Math.PI) / 180;
const Δφ = ((lat2 - lat1) * Math.PI) / 180;
const Δλ = ((lon2 - lon1) * Math.PI) / 180;
const h = Math.pow(Math.sin(Δφ / 2), 2) + Math.pow(Math.sin(Δλ / 2), 2) * Math.cos(φ1) * Math.cos(φ2);
return R * 2 * Math.asin(Math.min(1, Math.sqrt(h)));
}서울-뉴욕
HaversineFormula + atan : 11052555.8503412, 76.625 micro seconds
HaversineFormula + asin : 11052555.850341199, 28.709 micro seconds
SphericalLawOfCosines : 11052555.850341197, 19.292 micro seconds
EquirectangularApproximation : 17337148.1737011, 18.041 micro seconds
서울-수원
HaversineFormula + atan : 32343.763840874522, 2.75 micro seconds
HaversineFormula + asin : 32343.763840874522, 1.875 micro seconds
SphericalLawOfCosines : 32343.763840997413, 1.833 micro seconds
EquirectangularApproximation : 32343.76451538824, 1.292 micro seconds