Distance
개인적으로는 distance를 직접적으로 사용하는 경우는 많지 않았지만, 자주 사용하는 다른 함수 내부에서 사용하는 경우가 많아 먼저 살펴보고자 합니다.
Haversine formula
distance 함수의 주석을 보면 Haversine formula를 사용했다고 적혀있습니다. Haversine formula는 링크한 위키백과를 보시면 상세하게 설명되어 있습니다. 이 공식이 어떻게 도출되는지 찾아보고 이해해보려고 했지만 아직은 능력 밖의 일인지 여간 쉽지 않아서 주어진 공식으로 함수만 이해해 보려고 합니다.
우선 앞으로 공식에서 보게 될 는 두 점(P, Q) 사이의 거리인 에서 반지름인 을 나눈 라디안입니다.
Haversine 공식은 상단과 같은데 이때 두 점에 대해서 , 는 경도(latitude)를 , 는 위도(longitude)를 나타내며 단위는 라이안입니다.
Haversine 공식을 상단과 같이 나타낼 수 있는데, 이 공식은 Versine 문서를 보면 확인할 수 있습니다.
Haversine은 versine의 절반을 의미하며 상단의 그림을 통해 versine은 임을 알 수 있음으로 아래와 같은 식을 도출할 수 있습니다.
Haversine의 역함수를 취하여 를 구하고 가 임을 사용하면 우리가 구하고자 했던 두 점 사이의 거리인 를 얻을 수 있습니다. 는 로 대치될 수 있는데 이 부분은 Versine - Inverse functions 문서를 참조하시길 바랍니다.
Code
function distance(
from: Coord,
to: Coord,
options: {
units?: Units;
} = {}
) {
var coordinates1 = getCoord(from);
var coordinates2 = getCoord(to);
var dLat = degreesToRadians(coordinates2[1] - coordinates1[1]); var dLon = degreesToRadians(coordinates2[0] - coordinates1[0]); var lat1 = degreesToRadians(coordinates1[1]); var lat2 = degreesToRadians(coordinates2[1]);
var a = Math.pow(Math.sin(dLat / 2), 2) + Math.pow(Math.sin(dLon / 2), 2) * Math.cos(lat1) * Math.cos(lat2);
return radiansToLength( 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a)), options.units );}앞선 섹션에서 Haversine에 대해 살펴봤으니, 이제 코드를 살펴보고자 합니다. 코드는 상단에 표시한 것과 같이 크게 세 개의 파트로 나누어 살펴보고자 합니다.
var dLat = degreesToRadians(coordinates2[1] - coordinates1[1]);
var dLon = degreesToRadians(coordinates2[0] - coordinates1[0]);
var lat1 = degreesToRadians(coordinates1[1]);
var lat2 = degreesToRadians(coordinates2[1]);이 부분은 다음 파트에서 사용할 삼각 함수들에서는 육십분법(도, ) 대신 라디안을 사용하기 때문에, 다음 파트를 위한 준비 작업으로 봐주시면 될 것 같습니다.
var a =
Math.pow(Math.sin(dLat / 2), 2) +
Math.pow(Math.sin(dLon / 2), 2) * Math.cos(lat1) * Math.cos(lat2);이 부분은 앞서 살펴본 의 archaversine에 들어갈 를 구하는 부분입니다. 앞선 섹션에서 살펴보았다시피 는 아래와 같은 수식으로 구해지게 됩니다.
return radiansToLength(
2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a)), options.units
);마지막 부분은 을 참고하면, 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a))를 통해 를 구하고, radiansToLength의 내부에서 을 단위에 맞추어 변환하여 에 곱해 를 구하는 것을 확인할 수 있습니다.
여기서 한 가지 의문점이 발생했는데, 앞서 살펴보았던 Haversine 공식인 에서 arcsine을 사용했지만 코드에서는 arctangent를 사용하고 있다는 점입니다. 이 부분에서 arcsine 대신 arctangent를 사용하는 부분의 연결 고리가 잘 파악되지 않아 여러 사이트를 찾아가며 확인했습니다.
우선 arcsine에서 arctangent로 변환하는 과정은 Inverse trigonometric functions - Relationships among the inverse trigonometric functions를 참조하여 아래와 같이 변환되었음을 확인하였습니다.
변환 방법은 이해가 되었지만, 왜 변환을 했는지에 대한 의문은 풀리지 않았습니다. Haversine 공식에 대한 문서에서는 부동소수점 문제로 인해 가 로 범위가 제한된다고 적혀있었지만 명확하게 느낌이 오지 않아 계속 찾아보았습니다. 결론부터 말씀드리자면, 코드의 주석에 Calculate distance, bearing and more between Latitude/Longitude points라는 글을 같이 안내하고 있었음에도 불구하고 필자가 가볍게 훑어보고 넘긴 부분이 이곳저곳을 더 헤메게 만들었습니다.
필자가 이 부분에 대해 개인적으로 정리한 부분은 를 계산하는 과정에 그 값이 0.333333333334 + 0.666666666667과 같은 값이 되었을 때, 부동소수점 문제로 인해 이 값이 1을 넘겨버릴 경우 발생하게 되고, 이럴 경우 arcsine을 사용하여 값을 가져올 수 없기 때문이라고 생각했습니다. 그래서 arcsine을 사용하면 이를 해결하기 위한 처리가 별도로 필요하기 때문에 arctangent를 사용한 것으로 결론을 내렸습니다. 앞서 언급한 문서에도 만약 arctangent를 사용할 수 없는 경우라면 아래와 같이 앞서 말한 부분을 적용해서 arcsine을 사용하도록 가이드를 하고 있습니다.
return radiansToLength(
2 * Math.asin(Math.min(1, Math.sqrt(a))), options.units
);상단의 코드와 같이 Math.asin을 사용할 때, 범위 을 벗어나는 것을 막기 위해 Math.min을 사용한 방어 코드를 사용함을 확인할 수 있습니다.
참고 문서
- Haversine formula - 위키백과
- Calculate distance, bearing and more between Latitude/Longitude points
- Great-circle distance - 위키백과
- Spherical law of cosines - 위키백과
- Vincenty’s formulae - 위키백과
- 코사인 법칙 - 위키백과
- 최단거리 구하기, 하버사인 공식(Haversine Formula)
- [Alogrithm] 지구에서 두 점 사이의 거리 구하기
- Why Are Great Circles the Shortest Flight Path?
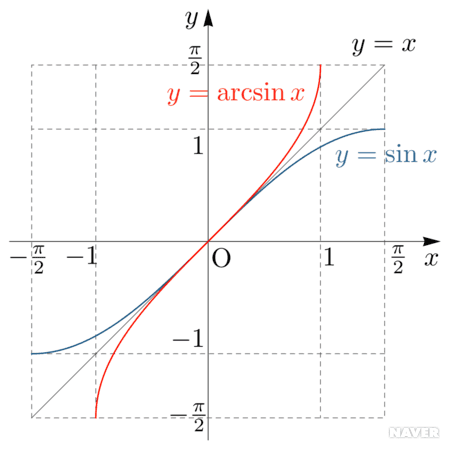
- 아크사인 - 네이버 수학백과