Bearing
주로 Line 위에 방향을 표시할 때 많이 사용했고 Along 내부에서 사용하는 Bearing에 대해 살펴보고자 합니다.
Great-circle distance
Bearing도 Distance와 유사하게 Haversine formula와 Great-circle distance와 관련이 있습니다.
baghdad-to-osaka - www.movable-type.co.uk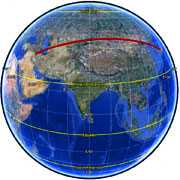
다음과 같이 두 점사의 각도를 살펴보면 Great-circle distance에 의해 다음과 같이 두 점 사이의 각도를 구할 수 있습니다. 이때 두 점에 대해서 , 는 경도(latitude)를 , 는 위도(longitude)를 나타내며 단위는 라이안입니다.
하지만 cosine의 경우는 부동소수점에 의한 반올림 이슈가 발생할 수 있어서 다음과 같이 Haversine Formula을 사용한다고 합니다.
앞서 살펴본 arcsine을 사용하는 방식은 대적점에서 반올림 문제로 고통받을 수 있어, 더 정확하게 구할 수 있는 Vincenty formula를 사용한다고 합니다. Vincenty formula는 장축과 단축이 동일하다면 사용할 수 있음으로 turf.js에서는 지구를 반지름이 동일한 구로 가정하고 있어 이를 사용한 것으로 보입니다. Vincenty formula는 해당 내용만으로도 살펴볼 것이 많아 따로 시간을 내어 공부해보고자 합니다.
Code
export default function bearing(
start: Coord,
end: Coord,
options: {
final?: boolean;
} = {}
): number {
// Reverse calculation
if (options.final === true) {
return calculateFinalBearing(start, end);
}
const coordinates1 = getCoord(start);
const coordinates2 = getCoord(end);
const lon1 = degreesToRadians(coordinates1[0]);
const lon2 = degreesToRadians(coordinates2[0]);
const lat1 = degreesToRadians(coordinates1[1]);
const lat2 = degreesToRadians(coordinates2[1]);
const a = Math.sin(lon2 - lon1) * Math.cos(lat2);
const b =
Math.cos(lat1) * Math.sin(lat2) -
Math.sin(lat1) * Math.cos(lat2) * Math.cos(lon2 - lon1);
return radiansToDegrees(Math.atan2(a, b));
}
function calculateFinalBearing(start: Coord, end: Coord) {
// Swap start & end
let bear = bearing(end, start);
bear = (bear + 180) % 360;
return bear;
}이제 앞서 살펴본 내용에 대한 코드의 구현을 살펴보겠습니다.
if (options.final === true) {
return calculateFinalBearing(start, end);
}이 부분은 final을 옵션으로 받아 그 값이 참이면 bearing의 결과로 받은 각도를 0~360으로 변경해줍니다.
const coordinates1 = getCoord(start);
const coordinates2 = getCoord(end);
const lon1 = degreesToRadians(coordinates1[0]);
const lon2 = degreesToRadians(coordinates2[0]);
const lat1 = degreesToRadians(coordinates1[1]);
const lat2 = degreesToRadians(coordinates2[1]);다른 글들을 통해 계속 보아오던 함수들과 동일하게 좌표에 대해 미리 각도를 육십분법에서 라디안으로 변경하는 직업을 수행합니다.
const a = Math.sin(lon2 - lon1) * Math.cos(lat2);
const b =
Math.cos(lat1) * Math.sin(lat2) -
Math.sin(lat1) * Math.cos(lat2) * Math.cos(lon2 - lon1);
return radiansToDegrees(Math.atan2(a, b));a와 b를 구해 Math.atan2(a, b)에 넣는 부분이 Vincenty formula에 해당하는 것으로 보이지만 Vincenty formula에 대한 이해가 부족하여 어떻게 도출되는지 명확하게 이해되지 않았습니다. Great-circle distance와 Vincenty formula의 문서에 일부 해당 값들을 통해 노출되는데 이 부분은 Vincenty formula에 대해 별도로 공부를 해봐야 이해가 갈 것 같아 이쯤에서 마무리하고자 합니다.