필드
필드(Field, 체)
대수적 구조의 하나로 사칙연산을 집합 안에서 소화할 수 있는 집합을 의미한다(연산의 결과 또한 해당 집합의 원소). 체에 대한 기본적인 예시로는 유리수의 집합(), 실수의 집합(), 복소수의 집합() 등이 있으며, 나눗셈을 하였을 때 나누어 떨어지지 않는 정수의 집합()은 체가 되지 않는다.
Ref
- Ch2 - 43p
복소수(Complex number)
실수만 고려하면 의 해를 찾을 수 없다. 이런 문제를 해결하기 위해 수학자들은 를 도입하였으며, 이는 보통 -1의 제곱근으로 정의된다. 실수와 의 곱은 허수(imaginary number)라고 한다.
식 에 대한 해는 이며, 이와 같은 실수와 허수의 합을 복소수라 한다.
Ref
- Ch2 - 43p
필드의 추상화
- 개념, theorem, 프로시저를 산술 연산자 , , , 에 대해 기술한다.
- 이들 연산자는 교환법칙, 결합법칙과 같은 기본적 법칙만을 만족한다고 가정한다.
개념, theorem, 프로시저는 이들 기본 법칙에만 의존하므로, 필드라 불리는 임의의 수 체계에 적용할 수 있다.
Ref
- Ch2 - 45p
복소수 필드
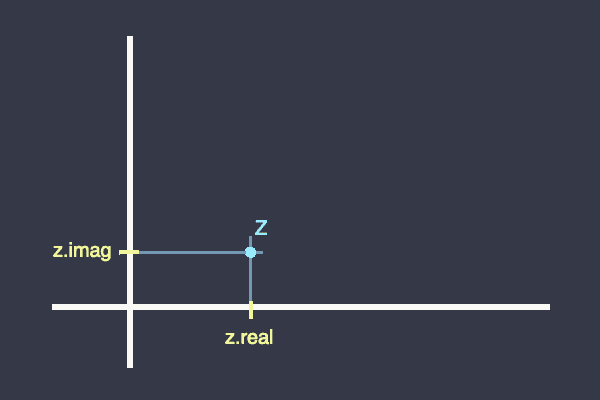
각 복소수 는 두 개의 일반적인 수 과 로 이루어지며, 전통적으로 는 평면(복소평면) 위의 어떤 점, 위치를 명시한다고 생각한다.
복소수의 절대값
복소수 z의 절대값()은 복소 평면의 원점에서 대응하는 점까지의 거리를 말하는데, 이는 피타고라서 정리에 의해서 이다.
공액 복소수(Definition 2.4.2)
복소수 의 공액 복소수는 로 쓰며, 로 정의된다. 이란 사실을 이용하면 에 대한 식을 얻을 수 있다.
복소수 덧셈하기
복소수들에 대한 평행이동은 와 같은 형태를 가지며, 여기서 는 복소수이고 이에 의해 평행이동을 한다.
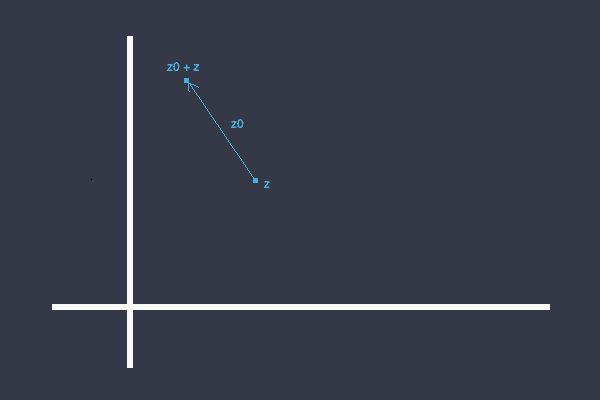
복소수를 화살표로 그리기
화살표의 꼬리는 복소 평면의 임의의 점 에 위치하고 화살표의 머리는 가 이동한 점 에 위치한다(이 표현이 고유한 것은 아님). 평행이동은 형태를 가지므로, 평행이동은 에 의해 표현된다.
평행이동 합성하기, 화살표 더하기
와 를 두 개의 평행이동이라 할 때, 이 둘을 합성하면 에 의해 정의되는 또 다른 평행이동이 만들어진다.
Complex Number Field - Composition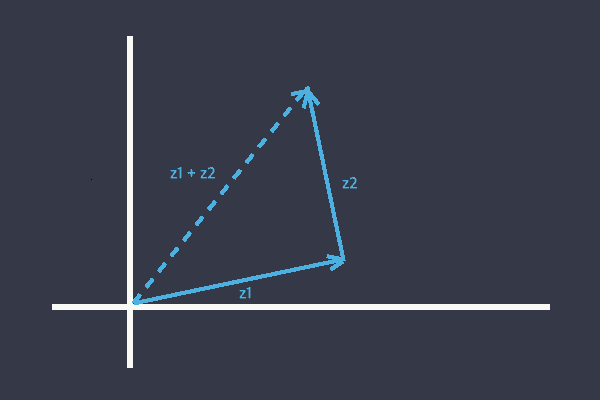
양의 실수로 복소수 곱하기
복소수에 양의 실수를 곱하면, 각 복소수의 실수 좌표와 허수 좌표의 크기를 변경해 그래프의 크기를 변경한다. 이를 스케일링(scaling)이라고 한다.
음수로 복소수 곱하기: 180도 회전
복소수에 음수 -1을 곱하면 원점 주위를 180도 회전한다.
를 곱하기 : 90도 회전
도형을 90도 회전하고자 한다면 에 위치한 점을 로 움직이면 된다. 에 위치한 복소수는 이므로, 라는 사실을 이용하여 에 를 곱하여 를 얻어낸다. 이때 이를 점으로 나타내면 이다.
복소 평면의 단위원: 편각(argument)과 각도(angle)
180 또는 90도의 회전이외에 어떠한 회전도 복소수 곱에 의해 표현할 수 있다. 하지만, 회전 각도의 측도로 각도(angle) 대신 라디언(radian)을 사용하는 것이 편리하다.
단위원 위에 있는 복소수의 편각
단위원은 복소 평면의 원점에 중심을 둔 반지름 1인 원이다.
Complex Number Field - Unit Circle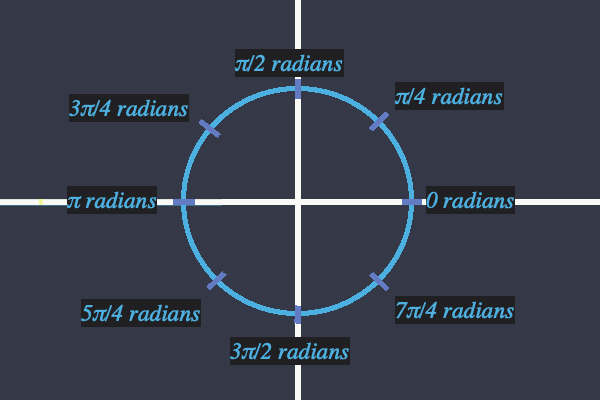
원위의 점 는 원의 가장 오른쪽 점인 에서 시작하여 에 도달할 때까지 원을 따라 반시계 방향으로 이동하는 거리로 표현되는데 이러한 거리를 의 편각이라 한다.
Complex Number Field - Argument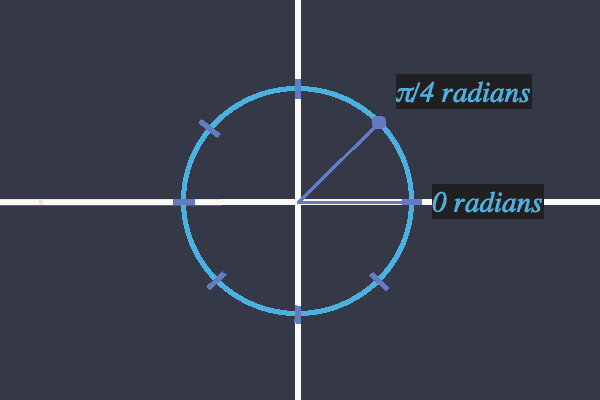
단위원 위의 두 복소수에 의해 형성된 각도
단위원 위의 두 점 사이에 형성된 각도에 숫자를 할당할 수 있고 이는 라디안으로 표현된다. 이때 이 각도는 두 점 사이를 반시계 방향으로 원을 따라 이동한 거리이다.
Complex Number Field - Argument between points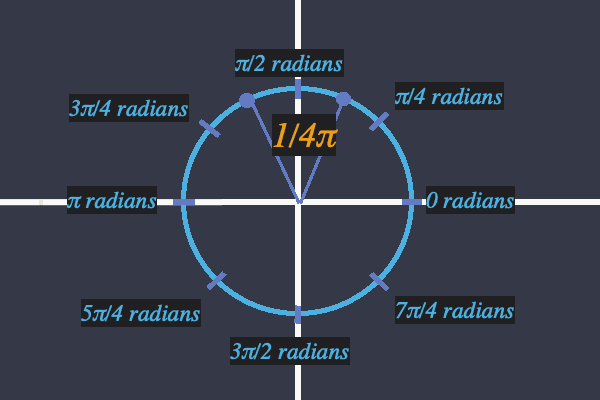
오일러 공식
오일러 공식은 임의의 실수 에 대해, 는 편각이 인 단위원의 점 라는 것을 의미한다(여기서 는 초월수(transcendetal number)이다). 오일러 공식은 단위원 위에 있는 복소수를 쉽게 표현할 수 있는 방법을 제시한다.
예를 들어 의 편각 를 오일러 공시에 대입하면, 을 얻을 수 있다.
복소수에 대한 극좌표 표현
을 원점에서 까지의 복소 평면 위에 있는 선분이라 하면, 은 이 성분이 단위원과 교차하는 점이라고 하고 은 까지의 선분의 길이라고 할 때, 다음과 같이 쓸 수 있다.
Complex Number Field - Polar Coordinate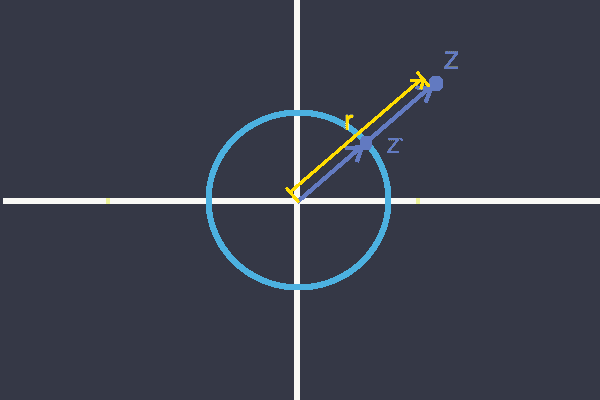
여기서 과 는 의 극좌표이며, 의 절대값()은 이라고 정의한다.
첫 번째 지수 법칙
지수에 대한 곱은 그 지수들을 더하면 되는데, 이 규칙은 복소수 를 어떻게 회전시키는지 이해하는데 도움을 준다.
라디안 회전
를 라디안 값이라 할때, 를 만큼 회전한 것은 와 절대값은 같고 편각은 보다 만큼 더 커야한다. 즉, 만큼 회전한 는 이다.
따라서 만큼 회전한 것을 나타내는 함수는 단순히 다음과 같이 쓸 수 있다.
연산 결합하기
복소수는 필드를 형성하므로, 익숙한 대수적 규칙들을 사용할 수 있다. (결합법칙 등…)
Ref
- Ch2 - 46~58p
- 갈루아 필드(Galois Field 2)
필드는 두 개의 원소 과 를 가지며, 아래의 두 표를 만족한다.
덧셈과 뺄셈은 modulo 2 이며 배타적 논리합(exlusive-or)과 같다.
곱셈과 나눗셈은 일반적인 과 의 산술 연산과 같다.
Ref
- Ch2 - 58p